AGS Performance with no PGNCS Alignment During the Homann Transfer (Task 46)

R. Brodreau12 July 196868:7252.8.222R. KiddAGS Performance with no PGNCS Alignment During the Homann Transfer (Task 46)

References: 1. LM AGS Guidance Software Design Report No. 3, TRW 05952 TRW 05952-6079-T000, 30 November, 1966.

2. Master End Item Specification for Lunar Module PGNCS.

Introduction and Summary

There is some concern about the capability of the AGS to safely perform an abort from hover without a PGNCS alignment during the Hohmann transfer. This concern stems from the results of Monte Carlo analyses which indicate that the mean minus three sigma for perilune altitude of an AGS controlled abort from hover is less than 30,000 feet (the safe orbit limit), and from single error analyses which indicate that an initial misalignment slightly larger than three sigma results in an unsafe orbit. Obviously, the effect of eliminating the PGNCS alignment during the Hohmann transfer is to increase the probability of obtaining an unsafe abort orbit. However, the rough analysis presented herein indicates that the increase in probability is on the order of .001 times the probability of a PGNCS failure during the powered descent maneuver, and the decrease in the mean minus three sigma for the perilune altitude of a hover abort is about 3000 feet. Since the PGNCS alignment during the Hohmann transfer would require RCS propellant, time allocated for the correction of erroneous star sightings, and no insignificant amount of crew activity, the gain in safe orbit probability provided by the alignment does not appear to be worth the operational complexity of performing the alignment. However, the AGS performance specifications may need to be changed because the AGS performance capability will be degraded if the PGNCS alignment during the Hohmann transfer is eliminated.

Discussion

The probability that an unsuccessful abort results from a working AGS is given by:

⌠ᵀ P(σ_ο) = ⌡_ο f(t) P₁ (t,σ_ο) dt

where

(ο,T) is the time interval of powered descent, σ_ο is the standard deviation of the initial AGS alignment error, f(t) is the probability density function for the occurrence of an AGS controlled abort, P₁ (t, σ_ο) is the probability than at AGS controlled abort at time t will not be safe.

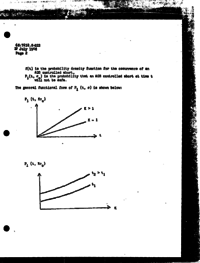
The general functional form of P₁ (t, σ_ο) is show below:

[Illustration omitted]

[Illustration omitted]

Since P₁ (t, σ_ο) is a positive, continuous, non-decreasing function of t,

⌠ᵀ P (σ_ο) = P₁ (T, σ_ο) ⌡_ζ (t) dt = P₁ (T, σ_ο) F (ζ, T)

where

P₁ (t, σ_ο) is the probability than at AGS controlled abort at time t will not be safe.

F (ζ, T) is the probability that an AGS controlled abort will be required during the interval F(ζ, T).

Generally, the following observations hold:

◦ An AGS controlled abort is required only for a PGNCS failure; and hence, F (ζ, T) is the probability of a PGNCS failure during the interval (ζ, T)

◦ The probability of an unsafe abort is less than or equal to the probability of an abort occurring – equality requires that P₁ = 1.

◦ The increase in the probability of an unsafe abort resulting from no alignment during the Hohmann transfer is less then the increase in P₁ (t, σ_ο) by the factor F (ζ, T).

◦ The probability P₁ (t, σ_ο), is not a known analytical or tabular function; however, the random Monte Carlo samples which have been generated follow a normal distribution very closely (reference 1). Hence a normal distribution is a reasonable approximation for a qualitative assessment.

The functional form for the variation in perilune altitude is approximately (reference 1).

R_p = A_e + _eᵀ D_e + 60,000

Where,

_e is the vector of random errors such as misalignment, accelerometer bias, etc.

A, D are matrices of first and second order coefficients, respectively.

For independent, normally distributed errors with zero mean and standard deviations σ_i, the mean and standard deviation for R_p are:

μ = ∑ d_i σ_i² + 60,000 σ² = ∑ a_i² σ_i² + 2 ∑ d_i² σ_i⁴

The effect of the initial AGS alignment accuracy on the mean and standard deviation of the perilune altitude for a hover abort was computed from the data available in the referenced document (inflight calibration error model). These results are shown on the attached figure. The initial AGS misalignment is the root sum square of the following.

◦ PGNCS alignment accuracy 1σ ≈ 3.43 min (Reference 2)

◦ PGNCS gyro drift from previous alignment 1σ ≈ 0.3 deg/hr (Reference 2)

◦ AGS to PGNCS alignment transfer 1σ ≈ 1.3 min (Reference 1)

The mean, standard deviation, and probability that the hover abort perilune altitude is less than 30,000 feet (unsafe) were obtained from the attached figure and standard statistics tables (assumed a normal distribution) for three alignment times of interest, and are tabulated below.

Statistics for Hover Abort Perilune

Total time AGS Align Perilune Perilune Probability Mean Minus for PGNCS Accuracy Altitude Altitude that R_ο 3 Sigma Drift (Hrs) σ_ο (min) Mean (ft) Sigma (ft) <30,000 (ft)

0.25 3.70 59,288. 7939. .00011 35,471. 0.50 3.78 59,274. 8029. .00013 35,187. 1.50 4.56 59,121. 8952. .00079 32,265.

Conclusions

The statistics from the above table indicate that eliminating the PGNCS alignment during the Hohmann transfer increases the probability of obtaining an unsafe perilune by 6.8 x 10⁻⁴ times the probability of a PGNCS failure and decreases the mean minus three sigma for the hover abort perilune by 3206 feet. These changes are based upon the particular AGS error model available at the tine the referenced analysis was performed. However, it appears reasonable to assume that the changes based upon the current error model would be of the same order of magnitude, i.e.: 10⁻³ for the probability and 3000 feet for the perilune. This small loss in AGS performance should be worth the operational gains of eliminating the PGNCS alignment